Постановка проблемной алгоритмической задачиandr писал(а):
Дано1)
Многоразрядный двоичный сумматор - для простоты - 4-х разрядный:
Вложение:
Вложение ПарСумматор.PNG больше недоступно
(продолжение следует)
Данный сумматор размещается в арифметико-логическом устройстве центрального процессора.
Это более или менее характерная схема (удобная для отражения общих принципов).
Но на самом деле для параллельных сумматоров существует много разных типов и разных конструктивных решений.
2) Традиционное описание таких устройств в учебниках включает в себя:
а)
Схемно-аналитическое представление (с формулами):
многоразрядного сумматора в целом и составляющих его одноразрядных сумматоров.
б) Сопутствующее словесное описание его
устройства и работы.
в) Иногда приводятся временные диаграммы работы конкретной аппаратуры:
на уровне работы конкретного конструктора-схемотехника - во всех деталях,
но не с целью отражения обобщенных (теоретических) принципов работы
(громоздкие и плохо понятные для уяснения сути дела).
Примерно также обстоит вопрос - по опыту общения с проектной документацией печатных плат в КБ
(но небольшой опыт).
Года три был опыт проведения по совместительству лабораторных работ (за компьютером)
в составе общего курса по цифровой схемотехнике (для специальности САПР).
Надо (очень проблемные вопросы):
1) Выяснить, почему (по каким причинам) используются:
словесное в основном описание работы сумматора
и не очень подходящие для понимания (алгоритмического) принципа действия
временные диаграммы (перегруженные частной детализацией).
2) Предложить
алгоритмический способ описания работыпараллельных сумматоров с последовательным межразрядным переносом.
-------------------------------------------------------------------------------
Всего лишь - предложить алгоритмическое описание.
И чего это никто не додумался?
А может быть это уже
используется где-то в теории, в проектировании или в обучении,
но это не является общеизвестным и общедоступным?
-------------------------------------------------------------------------------
Ответ (ответы - кратко и в предварительной идее).
Укрупненный общий алгоритм работы схемы включает три этапа - это так или иначе используется в словесном описании:
запись данных (из оперативной памяти) во входные регистры A и B - складываемые двоичные числа a и b;
обработка данных сумматором - сложение двоичных чисел: a + b = s;
считывание результата s из выходного регистра S (в оперативную память).
Этот укрупненный алгоритм выполняется по управлением Устройства управления центрального процессора.
Его вполне
можно отобразить простой блок-схемойи
привести предельно упрощенную временную диаграмму исполнения алгоритмов.
Здесь пока нет никаких проблем.
Но
почему это не делается? - это совершенно не понятно
(по крайней мере нигде это не приходилось видеть).
-----------------------------------
Основная проблема начинается далее.
Работа самого параллельного сумматора выполняется полностью
самостоятельно - без управления
со стороны управляющего устройства процессора.
Это происходит потому, что параллельный сумматор выполняется как
(сложная)
комбинационная схема (комбинационный автомат) логического управления - на двоичной логике.
При этом для комбинационных логических схем (комбинационных логических автоматов) не применяется алгоритмическое описание их работы:
-- используются булевы функции
-- и, что не всегда, временные диаграммы их исполнения во времени:
с учетом длительности операций во времени и разных возможных проблем.
В асинхронных схемах могут возникать так называемые гонки процессов - с появлением кратковременных ложных срабатываний на выходах.
В процессорах обычно применяются синхронные логические схемы:
проблемы гонок можно избежать, но синхронная реализация булевых функций сложнее.
-------------------------------------------
Многоразрядный параллельный сумматор состоит из параллельно работающих (параллельно соединенных)
однорарядных сумматоров с их последовательное (поперечной) связью межразрядных переносов.
Одноразрядные сумматоры строятся на основе
полусумматоров для сложения двух одноразрядных чисел:
Вложение:
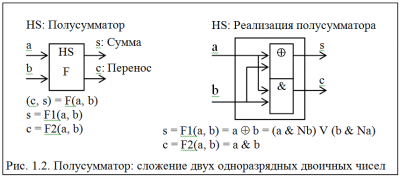 Полусумматор.PNG [ 22.88 КБ | Просмотров: 12464 ]
Полусумматор.PNG [ 22.88 КБ | Просмотров: 12464 ]
Некоторые схемы одноразрядных сумматоров
содержат по два последовательного связанных полусумматоров.
--------------------------------------------------------------------------
В статье:
http://paralg.ucoz.com/g4110/v5-g4110-s ... blasti.pdfИсторические области и парадоксы параллельной (и последовательной) алгоритмики приводятся примеры принципиальной возможности применения алгоритмов
для описания работы комбинационных схем - в данном случае для синхронных схем сумматоров
Вложение:
 Пример - текст.PNG [ 77.25 КБ | Просмотров: 12464 ]
Пример - текст.PNG [ 77.25 КБ | Просмотров: 12464 ]
Вложение:
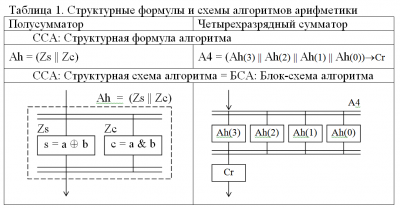 СФА и ССА.PNG [ 36.73 КБ | Просмотров: 12464 ]
СФА и ССА.PNG [ 36.73 КБ | Просмотров: 12464 ]
Здесь предполагается, что в параллельных ветвях алгоритмов длительность процессов одинакова
(как и на самом деле).
Если она не одинакова, то для исключения гонок процессов и ложных срабатываний выходов
длина синхронных цепей выравнивается, как это принято, вставкой повторителей
(элементов Или с объединенными входами).
В данном случае показано как сначала параллельно отрабатывают первые полусумматоры
в составе всех одноразрядных сумматоров,
затем начинается отработка межразрядных переносов.
После первого параллельного рада отработки первых полусумматоров
можно показать параллельный ряд отработки вторых полусумматоров
с появлением сигналов переносов на выходах одноразрядных сумматоров,
и после этого будет последовательное продвижение межразрядных переносов далее вдоль всех разрядов.
Все это можно четко фиксировать цифровыми протоколами хода счета
типа параллельного сложения столбиком (определенная модификация):
экспериментировать с разными парами двоичных чисел.
==============================
Очевидно, что все это необходимо четко обосновывать.
Предполагается подготовка подробной публикации по этой теме.
В данном случае привидится пример такой принципиальной возможности
(здесь могут быть варианты).
Возможно, что где-то кто-то уже (давно может быть) также печется по этому алгоритмическому поводу.
Но пока нигде не видел.



